Union-Find

Union-Find

알고리즘 회고 글에서 나열해놓은 순서대로 글을 작성하려 했지만, 오늘 본 코딩테스트에서 Union-Find 문제가 나왔는데 사소한 실수를 끝까지 못찾아 시간을 낭비했다.

그래서 반성하는 의미로 Union-Find를 먼저 정리하려고 한다.

Union-Find

Union-Find 알고리즘을 사용하는 이유는 매우 간단하다.

요소들을 정해진 규칙에 따라 그룹을 나누었을 때, A 요소와 B 요소가 같은 그룹에 속하는지 쉽게 알기 위한 알고리즘이다.

조금 더 정확히는 그래프 구조에서 같은 그룹에 속하는 지 빠르게 알기위해 필요한 알고리즘이다.

GROUP_A = [1,2,3]
GROUP_B = [4,5,6]
GROUP = {
    1:'A',
    2:'A',
    3:'A',
    4:'B',
    5:'B',
    6:'B'
}

그래프 구조에서 필요한 알고리즘이라고 한 이유는 위의 상황을 보면 알 수 있다.

위와 같이 그룹을 잘 표현한 자료구조가 만들어져있다면 굳이 다른 알고리즘 필요없이 시간복잡도 O(1)로 원하는 정보를 모두 알 수 있다.

이렇게 그래프 구조가 있을 때 1번 노드와 6번 노드가 같은 그룹에 있는지 알기 위해서는 어떻게 접근해야 할까?

1번 노드나 6번 노드를 시작점으로 반대 노드에 도달 할 때까지 노드를 이동하며 탐색해보고 도달 할 수 있다면 같은 그룹, 도달 할 수 없다면 다른 그룹이라고 알 수 있을 것이다.

그룹마다 노드의 개수가 많으면 관계를 한번 확인하는데 너무 많은 시간이 걸리기 때문에 이를 위한 알고리즘이 필요한 것이다.

Union-Find 알고리즘은 원리가 매우 간단하다. 각 그룹의 대표를 정하고 각자 자신의 대표를 저장하고 있으면 된다.

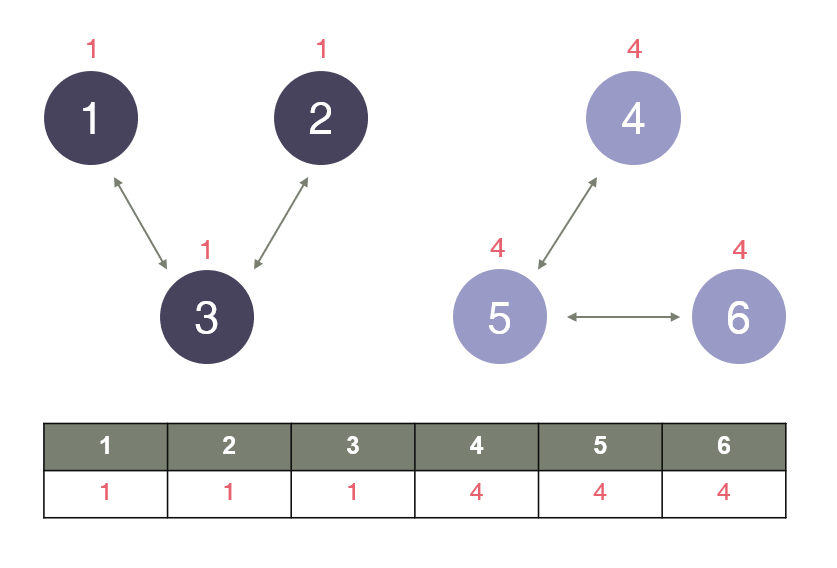
각 그룹에서 가장 작은 노드의 번호를 대표로 정하면 이런식으로 표현할 수 있다. (알고리즘 문제에 따라 대표를 정하는 방식이 중요하다)

이제 두 노드가 같은 그룹인지 확인하기 위해서는 자신의 속한 그룹의 대표가 서로 같은지만 비교하면 같은 그룹에 속하는지 알 수 있다.

이렇게 원리가 단순하기 때문에 Union-Find 알고리즘은 어떻게 구현하는가에 더 집중해야 한다.

Union-Find 구현

같은 그룹에 있는 6개의 노드의 대표를 지정하는 과정을 보면 Union-Find 알고리즘을 이해할 수 있을것이다.

대표를 정하는 기준은 그룹에서 가장 작은 노드의 번호로 한다.

임의의 노드에서 자신과 연결된 노드들을 탐색하며 기준에 따라 대표를 바꾸어 나가는 과정을 거쳐야 한다.(4번 노드에서 시작해보겠다)

우선 4번 노드에서 5번 노드로 이동해 둘을 한 그룹으로 묶고 값이 더 작은 4를 대표로 정했다.

이번엔 4번 노드에서 2번 노드로 이동해 둘을 한 그룹으로 묶고 대표를 정했다. 아마 여기서 의문이 한가지 발생할 것이다.

"지금까지 2, 4, 5번 노드를 한 그룹으로 묶었는데 5번의 대표가 혼자 다른데?" 이 의문은 Union-Find 과정이 모두 끝나고 나서 해결할 예정이다.

 

3번 노드와 6번 노드까지 이동해서 같은 과정을 진행하고 이제 1번 노드로 이동할 차례다.

여기서 주의해야할점은 1번 노드와 3번 노드를 비교한 후 3번 노드의 대표를 1로 바꾸면 안된다.

비교를 하는건 대표와 대표를 비교하는 과정이기 때문에 3번의 대표인 2와 1을 비교한 후 결과값은 2의 대표를 바꾸는 결과가 나와야한다.

결과는 우리가 기대했던 모든 대표값이 1이 나오는 모습과 많이 다르다. 이제 이전의 의문을 해결 할 차례다.

parents = [-1, 1, 2, 3, 4, 5, 6] # 현재 각자 자신의 부모(대표)가 자기 자신인 상태

def getParent(x):
	if(x == parents[x]): return x # 자기 자신이 부모와 같은 경우 그룹의 대표임을 의미한다.
	else: return getParent(parents[x]) # 재귀적으로 대표값이 나올 때 까지 부모를 따라 이동한다.

parents = [-1, 1, 1, 2, 2, 4, 4]

위에서 보여준것은 자신의 그룹 대표값을 1:1 대응으로 저장하고 있는것처럼 표현했지만 실제 구현해서는 재귀적으로 대표값에 도달할 때 까지 부모 노드를 따라 올라가야한다.

우선 자신의 값과 대표의 값이 같은 경우 자신이 대표라는 사실을 바탕으로 5번 노드에서 대표값을 찾아가보자.

5번 노드의 부모(대표)값은 4, 4번 노드가 대표인지 확인하기 위해 4번 노드의 부모값이 4인지 확인해보자. 4번 노드의 대표값은 2이기때문에 4번 노드는 대표가 아니다. 그러므로 계속해서 탐색해야 한다.

5 -> 4 -> 2 -> 1의 순서를 거쳐서 5번 노드가 속한 그룹의 대표값이 1번임을 알 수 있다.

Union-Find 알고리즘을 사용한 이유가 같은 그룹임을 빠르게 알고 싶어서 인데 이래서는 그렇게 빠르게 느껴지지 않을 수 있다.

노드를 직접 전부 탐색하는것에 비해서는 훨씬 빠르지만 재귀적으로 탐색하는것에 만족하지 못할 수 있다. 그래서 이를 위한 최적화 방법이 존재한다.

def getParent(x):
	if(x == parents[x]): return x 
	else: 
        parents[x] = getParent(parents[x]) #getParent로 탐색을 할 때마다 직접적으로 대표값을 가르키도록 업데이트 해줄 수 있다.
        return parents[x] 

위와 같은 최적화를 추가해준다면 한번 탐색한 이후 부터는 자신의 대표값을 바로 가르키게 업데이트 된다.

사실 Union-Find 알고리즘 문제를 풀어보면 이 최적화를 추가하지 않는다고 해서 시간초과가 나는 경우는 잘 없다.

def Union(x, y):
    px = getParent(x)
    py = getParent(y)
    if(px < py):
        parents[py] = px
    else:
        parents[px] = py

두 노드를 한 그룹으로 합치며 대표값을 갱신하기 위한 코드.

예시에서 3번 노드에서 1번 노드로 넘어갈 때 각 대표끼리 비교해야 한다고 했던 것을 기억해야 한다.

합치려는 노드의 대표들을 먼저 구한 후, 대표들의 값을 비교해 각자 대표의 부모값을 바꿔준다는 논리적인 흐름 그대로 구현을 해주면 된다.

def Union(x, y):
    px = getParent(x)
    py = getParent(y)
    if(value[px] < value[py]): #노드번호가 아닌 다른 기준에 의해 대표값을 정하고 싶을 때에는 이런식으로 변형 할 수 있다.
        parents[py] = px
    else:
        parents[px] = py
        
def getValue(x):
    return value[getParent(x)]

노드번호가 아니라 다른 기준으로 대표값을 정할 수 있다. 알고리즘 문제에 따라 이렇게 구현하는것이 도움이 될 때가 있다.

 

여담

def getParent(x): 
	if(x == parents[x]): return x 
	else: return getParent(parents[x]) # 원래 구현
	
def getParent(x):
	if(x == parents[x]): return x 
	else: return parents[parents[x]] # 오늘 실수한 부분

오늘 코딩테스트에서 아래와 같이 구현을 해버리고 어디서 틀렸는지 찾지 못하고 시간을 낭비했었다. 고쳐서 제출했다면 다행이었겠지만, 종료 5초전에 발견하고 급하게 고쳐서 제출을 눌렀는데 시간이 지나 제출하지 못했다...

Union-Find 문제는 풀어본적이 많아서 기계적으로 구현하고 있었기 때문에 오히려 getParent 함수를 의심하지 않았던 것 같다.